Distribución de frecuencia
3. Clase o intervalo de clase
4. Marca de clase
5. Histograma de frecuencia
6. Polígono de frecuencia
Para estudiar el comportamiento de un fenómeno se requiere información y esta se recopila
1) Por medio de encuestas (interrogatorio oral o escrito que se aplica a varias personas acerca del problema).
2) Por medio del registro de las observaciones que se hacen de él se obtienen los datos.

Entre los sistemas para ordenar los datos se encuentran principalmente dos:
4. Marca de clase
5. Histograma de frecuencia
6. Polígono de frecuencia
1. RECOPILACIÓN DE DATOS
Para estudiar el comportamiento de un fenómeno se requiere información y esta se recopila
1) Por medio de encuestas (interrogatorio oral o escrito que se aplica a varias personas acerca del problema).
2) Por medio del registro de las observaciones que se hacen de él se obtienen los datos.

Entre los sistemas para ordenar los datos se encuentran principalmente dos:
a)La distribución de frecuencias es un método para organizar y resumir datos en una tabla estadística .
b) La representación gráfica. Estos sistemas de organización y descripción de los datos permiten realizar un análisis de datos univariado, bivariado o trivariado, dependiendo de los objetivos y de la naturaleza de la investigación
2. TABLAS DE FRCUENCIAS
b) La representación gráfica. Estos sistemas de organización y descripción de los datos permiten realizar un análisis de datos univariado, bivariado o trivariado, dependiendo de los objetivos y de la naturaleza de la investigación
2. TABLAS DE FRCUENCIAS
DISTRIBUCIÓN
Una distribución de frecuencias constituye una tabla en el ámbito de investigación
La distribución de frecuencias puede ser simple o agrupada.
La distribución de frecuencias simple es una tabla que se construye con base en los siguientes datos: clase o variable (valores numéricos) en orden descendente o ascendente, tabulaciones o marcas de recuento y frecuencia.
La distribución de frecuencias agrupadas o acumulada es una tabla que contiene las columnas siguientes: intervalo de clase, puntos medios, tabulación frecuencias y frecuencias agrupadas.
DITRIBUCIÓN DE FRECUENCIAS SIMPLE
EJEMPLO A:Se preguntó a un grupo de 50 alumnos de Ingeniería Industrial su materia preferida.
EJEMPLO B:
Se preguntó a un grupo de 35 alumnos su estatura en cm.
Cuando los datos son cuantitativos y se presentan más de 15 valores diferentes, se recomienda resumir la información
Se distribuyen en grupos llamados clases o intervalos de clase y se determina el número de individuos que pertenecientes a cada clase, que es la frecuencia de clase.
EJEMPLO C:
La tabla que de tu derecha, es una distribución de frecuencias de alturas de un grupo de 100 estudiantes.
•La primera clase corresponde a la estatura de 60 a 62 y se representa 60 – 62.
•Su correspondiente frecuencia de clase es 5.
•Limites de los intervalos de clase
Tomando el primer intervalo de clase de la tabla que es 60 – 62.
• 60 es el límite inferior de clase. (menor)
•La primera clase corresponde a la estatura de 60 a 62 y se representa 60 – 62.
•Su correspondiente frecuencia de clase es 5.

•Limites de los intervalos de clase
Tomando el primer intervalo de clase de la tabla que es 60 – 62.
• 60 es el límite inferior de clase. (menor)

• 62 es el límite superior de clase. (mayor)

Límites reales.Es el resultado de restar 0,5 al límite inferior de clases y luego sumar esa misma cantidad al límite superior de clases.

En el intervalo 60 – 62 , teóricamente incluye todas las medidas desde 59,5000 hasta 62,5000
Estos números, representado breve por los números exacto 59,5 es el límite real inferior y 62,5 el límite real superior.
Hay una ambigüedad, pues los límites reales de clase no coincide con las observaciones reales . Así si una observación fuese de 62,5 no seria posible discernir si pertenece al primer intervalo o al segundo de la tabla”.
4. MARCA DE CLASE
Es el punto medio (X) de cada clase y se obtiene sumando los límites de clase y dividiéndolos entre dos. Representa el valor medio de cada clase.

Tamaño o anchura de clase
Es la diferencia entre los límites reales de clase, o la diferencia entre los límites de clase más una unidad (la misma que se esté trabajando) ó la diferencia entre las marcas de clase. Representa el numero de datos incluidos en el intervalo.

CONCLUSIÓN
Con lo anterior antes expuesto sobre lo concerniente a la tabla de distribución de frecuencia y utilizando el Ejemplo c: tabla de una distribución de frecuencias de alturas en pulgada de un grupo de 100 estudiantes. Podemos resumir en la siguiente tabla.
Con lo anterior antes expuesto sobre lo concerniente a la tabla de distribución de frecuencia y utilizando el Ejemplo c: tabla de una distribución de frecuencias de alturas en pulgada de un grupo de 100 estudiantes. Podemos resumir en la siguiente tabla.

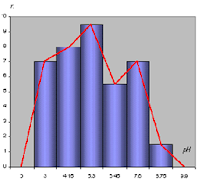
1. Un histograma o histograma de frecuencia consiste en una serie de rectángulos que tiene:
a) Su base sobre el eje horizontal (eje X) con centro en la marca de clase y longitud de igual tamaño de los intervalos de clase
b) Superficies proporcionales a la frecuencias.
a) Su base sobre el eje horizontal (eje X) con centro en la marca de clase y longitud de igual tamaño de los intervalos de clase
b) Superficies proporcionales a la frecuencias.




No hay comentarios:
Publicar un comentario